一、怎么理解积分这个概念?
开门见山,“积分”中的分字,就是微分、微小之意;积就是累积、加起来。顾名思义,积分就是把无穷多个无穷小累加起来合成一个整体。
对于微积分的理解、感悟,友友在《让你从根本上理解:微积分到底是什么?》一文中的留言评价有的非常好,读了让人受益匪浅、思路大开、体会深刻。现摘录几个共大家欣赏、感受、体会(我只是搬运,不代表我的观点哈)。
友友1:微分——用锉刀锉金属;积分——把锉碎的金属拢到一起。
友友2:微积分就是捭阖之术,既无限制地分下去,又可以阖一起。
友友3:微分研究函数局部细节,积分注重整体结果;做人何尝不是这样,持续努力,持续优化改进的人,结果一定也会比较好。
友友4:微积分是研究变化的科学,没有变化就不用微积分。导数是变化规律,无穷小是变化的趋势。积分是变化的累积。微积分是唯物辩证法的数学表现。
二、举例说明什么是微积分
1、初中阶段学过有关速度的公式

用符号表示,有
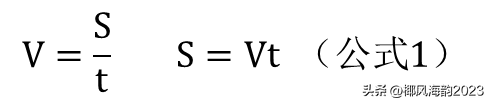
设想:你在操场上沿跑道跑步,跑了30秒,从100米处跑到了300米处,跑的距离是200米,那么你跑的平均速度约是6.67(米/秒)。
假设:你用大约6.67(米/秒)的速度匀速跑了30秒,则你跑的距离是
S=Vt=6.67Χ30=200(米)
实际情况:一般人跑步不可能一直是用平均速度匀速跑的,总会忽快忽慢,甚至会停下来喘口气。
问题:对于实际情况,跑的距离又该如何计算呢?
2、微积分的基础就是把整体进行分割,然后再求和得到整体
实际情况中,跑步速度随时间一直在变化不定,即速度是时间的函数:V=V(t),很明显,此时公式1不再适用。
不过,我们可以想办法继续使用公式1。
设跑步从时刻t1开始,到时刻t2停止,从x1处跑到了x2处。
为了使用公式1,可以把从t1到t2时间段分割成n个很小的有限小时间间隔:Δt1, Δt2, Δt3, ……, Δtn。
在每一个有限小时间间隔内,可以近似认为跑步是匀速的,其速度标记为V1, V2, V3, ……, Vn。
这样,在每个有限小时间间隔内,公式1仍然可以使用。对第i个有限小时间间隔Δti,其速度为Vi,字母i表示从1到n任意一个数字。则跑过的距离为
ΔSi≈ViΔti
跑过的总距离,是每个时间间隔内跑过的距离累加起来之和:
S≈ΔS1+ΔS2+……+ΔSi+……+ΔSn
=V1Δt1+ V2Δt2+ ……+ViΔti+……+VnΔtn

上式中的符号Σ是希腊字母,读作:西格玛,表示对后面内容求和的意思。
3、定积分
为了尽量减小近似计算带来的误差,很显然,分割出来的有限小时间间隔Δt越小越好,也即分割出来的Δt数量n越大越好。
越小越好的极限就是有限小变成无限小,无限小趋于0;n越大越好的极限就是n趋于无穷大∞。
当时间间隔Δt由有限小变成无限小时,我们知道公式2中的符号Δ应该换写成d;那么求和号Σ也不能原样不动,需要换个符号表示。
“求和”一词在英文中的词汇是sum,那么就把sum第一个字母S变形,写成ʃ的样子,表示对无穷多个无穷小求和的符号,称为积分号。
那么,公式2就可以改写成
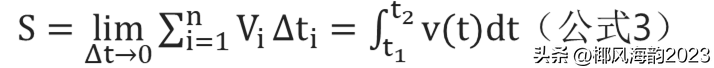
t1、t2分别称为积分的下限、上限。
公式3表示的积分,由于自变量有上、下限,这个积分有确定的值,故称为定积分。
4、积分效应
积分效应又称为累积效应,它最初用于对环境的影响评价。
人类活动或者自然变化在短时间内、或者偶尔出现,对环境产生的影响可能微不足道、不明显而被忽视或压根儿就察觉不到。但这些活动、变化如果次数多了或者持续时间长了,在长时间或者较大空间范围的影响就会逐渐显现出来。
比如大雾、空气污染等就是如此。
下图是清明节前,由于下雨而形成的大雾。

伸出手,看自己的手是清晰的,察觉不到雾的存在。但是大家都知道在眼睛和手之间雾是存在的,只是太过稀薄看不到罢了。随着距离的增加,雾对光的散射吸收作用逐渐明显,直到远处楼房、景物完全被雾遮挡,这就是雾的积分效应。
5、积分例题、不定积分
导数

求原函数f(t)。
解:由原题,有
df(t)=2tdt
对上式两边积分,有
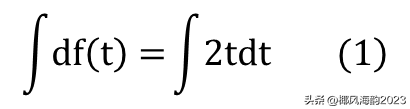
上式左边是对f(t)先微分,再积分,所以还是原来的函数f(t)
上式右边,由导数公式

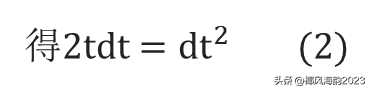
将(2)式代入(1)式:
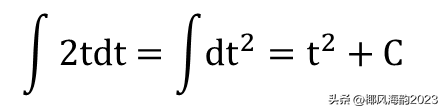
即原函数
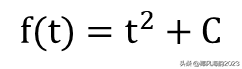
上面积分时没有确定上下限,这样的积分称为不定积分,字母C是任意常数。
因为常数的导数等于0,故对于任意常数C,上面求出的原函数的导数都一样,是2t。
如果确定了积分区间[t1,t2],则

与导数公式一样,常用积分公式也需要熟记,方便以后直接使用。
